مدارهای حرکت: تفاوت بین نسخهها
جز (در حال بازنگری (تا پایان صفحه ۱۹۰)) |
جز (تگ بیاولویت را برداشتم) |
||
| (۵ نسخهٔ میانیِ همین کاربر نمایش داده نشده است) | |||
| سطر ۶: | سطر ۶: | ||
[[Image:KHN003P192.jpg|thumb|alt= کتاب هفته شماره ۳ صفحه ۱۹۲|کتاب هفته شماره ۳ صفحه ۱۹۲]] | [[Image:KHN003P192.jpg|thumb|alt= کتاب هفته شماره ۳ صفحه ۱۹۲|کتاب هفته شماره ۳ صفحه ۱۹۲]] | ||
| − | |||
| − | |||
'''دکتر محسن هشترودی''' | '''دکتر محسن هشترودی''' | ||
| سطر ۳۹: | سطر ۳۷: | ||
'''مسیر قمر مصنوعی، دائرهئی است که مرکز آن، مرکز سیاره است. ''' | '''مسیر قمر مصنوعی، دائرهئی است که مرکز آن، مرکز سیاره است. ''' | ||
| − | این سرعت را، برای سهولت بیان، | + | این سرعت را، برای سهولت بیان، V۰ مینامیم. |
[طبیعی است که: اگر «ارتفاع جسم از سطح سیاره» تغییر کند، این سرعت نیز تغییر میکند، و هر چه ارتفاع جسم بیشتر شود، مقدار سرعت کمتر میشود. – یعنی: هر چه اقمار مصنوعی از سیاره دورتر باشند، سرعت دورانشان کمتر است. (فراموش نشود که، مسیر اقمار مصنوعی، '''دائره''' فرض شده است)] | [طبیعی است که: اگر «ارتفاع جسم از سطح سیاره» تغییر کند، این سرعت نیز تغییر میکند، و هر چه ارتفاع جسم بیشتر شود، مقدار سرعت کمتر میشود. – یعنی: هر چه اقمار مصنوعی از سیاره دورتر باشند، سرعت دورانشان کمتر است. (فراموش نشود که، مسیر اقمار مصنوعی، '''دائره''' فرض شده است)] | ||
| سطر ۴۶: | سطر ۴۴: | ||
==مسیرهای بیضوی== | ==مسیرهای بیضوی== | ||
| − | اساس قرار گرفتن قمر مصنوعی بر مدار، تعیین سرعت | + | اساس قرار گرفتن قمر مصنوعی بر مدار، تعیین سرعت V۰ است. بهاین معنی که، با سرعتهای کمتر از V۰ یا بیشتر از آن، میتوان مدارهای قمر مصنوعی را با مدار نظیر V۰ (یعنی مدار دایرهئی) سنجید و برحسب دوره گردش قمر مصنوعی بهگرد سیاره، مدار را مشخص کرد. |
| − | پس فرض کنیم که مدار دایرهٔ قمر مصنوعی که در ارتفاع معینی نسبت به سیاره دوران میکند، دایرهٔ C باشد. [سرعت حرکت، | + | پس فرض کنیم که مدار دایرهٔ قمر مصنوعی که در ارتفاع معینی نسبت به سیاره دوران میکند، دایرهٔ C باشد. [سرعت حرکت، V۰ است]. |
| − | اگر در همین ارتفاع، سرعت حرکت قمر مصنوعی در نقطهئی از مدار، کمتر از | + | اگر در همین ارتفاع، سرعت حرکت قمر مصنوعی در نقطهئی از مدار، کمتر از V۰ باشد، مسیر قمر مصنوعی دیگر دایره نیست. مسیر، بیضی است که دو نقطهٔ مفروض، با دایرهٔ پیش مماس است و تمام این بیضی در داخل دایرهٔ C قرار دارد. |
بنابراین، نقطهٔ مفروض مذکور، اوج قمر مصنوعی بر مدار است؛ و نقطهٔ مقابل، حضیض آن میباشد. | بنابراین، نقطهٔ مفروض مذکور، اوج قمر مصنوعی بر مدار است؛ و نقطهٔ مقابل، حضیض آن میباشد. | ||
| سطر ۵۶: | سطر ۵۴: | ||
==علل سقوط اقمار مصنوعی== | ==علل سقوط اقمار مصنوعی== | ||
| − | معمولاً با سرعتهای کمتر از | + | معمولاً با سرعتهای کمتر از V۰، این مدارها «مدار ساقط» هستند. یعنی قمر مصنوعی معمولاً پس از چند بار گردش، مجدداً برروی سیاره S سقوط میکند. |
| − | [این مسأله، غالباً بهعلت وجود جوی بر روی سیارهٔ مفروض است، که هرگاه قمر مصنوعی در حرکت خود وارد جو سیاره شود، بهعلت مقاومت این جو، سرعت قمر مصنوعی میکاهد و بالاخره با کاهش متوالی این سرعت، قمر مصنوعی به علت جاذبهٔ سیاره به آن نزدیک میشود و در نتیجه سقوط میکند و یا در همان برخورد اول با جو، میسوزد. | + | [این مسأله، غالباً بهعلت وجود جوی بر روی سیارهٔ مفروض است، که هرگاه قمر مصنوعی در حرکت خود وارد جو سیاره شود، بهعلت مقاومت این جو، سرعت قمر مصنوعی میکاهد و بالاخره با کاهش متوالی این سرعت، قمر مصنوعی به علت جاذبهٔ سیاره به آن نزدیک میشود و در نتیجه سقوط میکند و یا در همان برخورد اول با جو، میسوزد.] |
یک علت دیگر سقوط قمر مصنوعی این است که سیارهٔ مبداء، کرهٔ هندسی کامل نیست و با آن اختلاف دارد. زیرا محاسبات مدارهای اقمار مصنوعی، با این فرض که «سیارهٔ مبداء کروی است» صورت میگیرد؛ و اگر حاشیهٔ اطمینانی برای سرعت در نظر گرفته نشود، آخرالامر اختلالهائی که از اختلاف شکل سیارهٔ مبداء با «کرهٔ هندسی کامل» حاصل میشود، سرعت قمر را میکاهد. | یک علت دیگر سقوط قمر مصنوعی این است که سیارهٔ مبداء، کرهٔ هندسی کامل نیست و با آن اختلاف دارد. زیرا محاسبات مدارهای اقمار مصنوعی، با این فرض که «سیارهٔ مبداء کروی است» صورت میگیرد؛ و اگر حاشیهٔ اطمینانی برای سرعت در نظر گرفته نشود، آخرالامر اختلالهائی که از اختلاف شکل سیارهٔ مبداء با «کرهٔ هندسی کامل» حاصل میشود، سرعت قمر را میکاهد. | ||
| سطر ۶۵: | سطر ۶۳: | ||
این امر در اقمار مصنوعی امریکائی و شوروی رعایت شده است، و چنان که میدانیم، بسیاری از اقمار مصنوعی این دو کشور که به ماورای کرهٔ زمین پرتاب شدهاند مدتها بهدور زمین دوران کردهاند و یا میکنند. | این امر در اقمار مصنوعی امریکائی و شوروی رعایت شده است، و چنان که میدانیم، بسیاری از اقمار مصنوعی این دو کشور که به ماورای کرهٔ زمین پرتاب شدهاند مدتها بهدور زمین دوران کردهاند و یا میکنند. | ||
| − | |||
==مسیرهای «بالیستیک»== | ==مسیرهای «بالیستیک»== | ||
| سطر ۷۸: | سطر ۷۵: | ||
در شکل اول، کیفیت مدارهای بیضوی که در داخل مدار دایرهئی شکل قمر مصنوعی قرار دارند نشان داده شده است. | در شکل اول، کیفیت مدارهای بیضوی که در داخل مدار دایرهئی شکل قمر مصنوعی قرار دارند نشان داده شده است. | ||
| − | با سرعت V۰ در ارتفاع معین h، مدار دایره | + | با سرعت V۰ در ارتفاع معین h، مدار دایره c میباشد. |
سرعت V۱ حداقل سرعتی است که در ارتفاع h با آن سرعت قمر مصنوعی مدار بیضی شکل T۱ را میپیماید. | سرعت V۱ حداقل سرعتی است که در ارتفاع h با آن سرعت قمر مصنوعی مدار بیضی شکل T۱ را میپیماید. | ||
| − | بیضی T۱ | + | بیضی T۱ به جو سیاره ورود نمیکند و با آن مماس است. |
| − | مدارهای بیضی که بین T۱ و c واقعاند، مدارهای دوران میباشند (یعنی قمر مصنوعی برروی آنها | + | مدارهای بیضی که بین T۱ و c واقعاند، مدارهای دوران میباشند (یعنی قمر مصنوعی برروی آنها به دور سیاره دوران میکند). |
| − | مدارهای بیضی که درون T۱ میباشند، '''مدارهای ساقط''' هستند (یعنی قمر مصنوعی | + | مدارهای بیضی که درون T۱ میباشند، '''مدارهای ساقط''' هستند (یعنی قمر مصنوعی بر روی این مدارها& معمولاً پس از چند گردش، بالمآل بر روی سیاره سقوط میکنند). |
فرض کنیم که V۲ حداقل سرعتی است که مدار بیضی شکل قمر مصنوعی، در ارتفاع h با سطح سیاره مماس میشود؛ و این مدار بیضی شکل را T۲ مینامیم. مسیرهای بیضی که در اندرون بیضی T۲ واقعاند، به '''مسیرهای بالیستیک''' موسوماند. | فرض کنیم که V۲ حداقل سرعتی است که مدار بیضی شکل قمر مصنوعی، در ارتفاع h با سطح سیاره مماس میشود؛ و این مدار بیضی شکل را T۲ مینامیم. مسیرهای بیضی که در اندرون بیضی T۲ واقعاند، به '''مسیرهای بالیستیک''' موسوماند. | ||
نسخهٔ کنونی تا ۳۰ اکتبر ۲۰۱۷، ساعت ۰۹:۰۷
دکتر محسن هشترودی
مدارهای حرکت
قمر مصنوعی یا سفینهٔ فضایی
ممکن است از هر نقطهئی در مجاورت زمین، جسمی را بهسوی فضا پرتاب کنیم.
این جسم، برحسب آن که بهدور زمین بگردد یا بهگرد سیارهئی دوران کند و یا از سیارهئی [مثلاً سیارهٔ ما] بهسوی سیارهئی دیگر [مثلاً زهره] سفر نماید، قمر مصنوعی و یا سفینهٔ فضائی نامیده خواهد شد.
مسیر این قمر مصنوعی یا سفینهٔ فضائی را «امتداد اول حرکت» مشخص میکند. و غرض از «امتداد اول حرکت» امتدادی است که جسم، برروی آن پرتاب میشود... مثلاً اگر جسمی را از روی زمین بهطور قائم پرتاب کنیم. آن جسم برروی خط قائم صعود خواهد کرد و بعد، اگر سرعت آن کفایت نکند، پس از آن که بهاوج حرکت رسید برروی خط قائم سقوط کرده مجدداً بر زمین میافتد. – یا اگر جسمی را با همان سرعت برروی امتدادی مایل پرتاب کنیم، نخست برروی مسیری منحنی بالا میرود و پس از اوج، مجدداً بهصورت مایل بر زمین عودت میکند.
در این قسمت، فعلاً از اینکه جسمی را در ارتفاع معینی قرار بدهیم چشم میپوشیم. یعنی فرض میکنیم که جسم، قبلاً، بهوسیلهئی متناسب، در ارتفاع مورد نظر قرار گرفته است.
[بعدها خواهیم دید که برای قرار دادن قمر مصنوعی در مدار، یکی از مشکلات عمدهٔ کار، همین است. و این اشکال، هنگامی که سیارهٔ مبدا مانند زمین – دارای جوی بخاری باشد بیشتر میشود.]
مدارهای دائرهئیشکل
غرض از امتداد مماسی، امتدادی است عمود بر آن شعاع سیاره که بر این نقطه میگذرد.
در هر ارتفاعی، سرعتی وجود دارد که اگر جسم را با آن سرعت بر امتدادی مماسی پرتاب کنیم، جسم پرتاب شده، بر روی مدار دایرهئی شکل بهدور سیاره گردش میکند. بهعبارت دیگر:
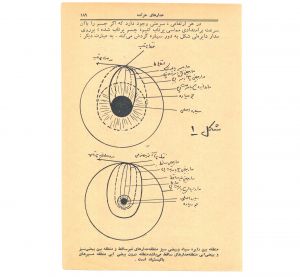
- توضیحِ شکلِ صفحهٔ ۱۸۹:
- شکل ۱: منطقه بین دایره سیاه و بیضی سبز منطقه مدارهای غیرساقط و منطقه بین بیضی سبز و بیضی آبی منطقه مدارهای ساقط میباشد. منطقه درون بیضی آبی منطقه مسیرهای بالیستیک است.
مسیر قمر مصنوعی، دائرهئی است که مرکز آن، مرکز سیاره است.
این سرعت را، برای سهولت بیان، V۰ مینامیم.
[طبیعی است که: اگر «ارتفاع جسم از سطح سیاره» تغییر کند، این سرعت نیز تغییر میکند، و هر چه ارتفاع جسم بیشتر شود، مقدار سرعت کمتر میشود. – یعنی: هر چه اقمار مصنوعی از سیاره دورتر باشند، سرعت دورانشان کمتر است. (فراموش نشود که، مسیر اقمار مصنوعی، دائره فرض شده است)]
در این قسمت، همواره فرض بر این است که قمر مصنوعی (یعنی جسم پرتاب شده از مجاورت سیارهٔ مفروض) از سیاره چندان دور نشده است که دیگر قوهٔ جاذبهٔ سیاره بر آن مؤثر نباشد؛ وگرنه جاذبهٔ سیارهٔ دیگر یا یک جسم فلکی دیگر، ممکن است قمر مصنوعی را بهکلی از مسیر خود منحرف کند و بهجانب خود متمایل سازد.
مسیرهای بیضوی
اساس قرار گرفتن قمر مصنوعی بر مدار، تعیین سرعت V۰ است. بهاین معنی که، با سرعتهای کمتر از V۰ یا بیشتر از آن، میتوان مدارهای قمر مصنوعی را با مدار نظیر V۰ (یعنی مدار دایرهئی) سنجید و برحسب دوره گردش قمر مصنوعی بهگرد سیاره، مدار را مشخص کرد.
پس فرض کنیم که مدار دایرهٔ قمر مصنوعی که در ارتفاع معینی نسبت به سیاره دوران میکند، دایرهٔ C باشد. [سرعت حرکت، V۰ است].
اگر در همین ارتفاع، سرعت حرکت قمر مصنوعی در نقطهئی از مدار، کمتر از V۰ باشد، مسیر قمر مصنوعی دیگر دایره نیست. مسیر، بیضی است که دو نقطهٔ مفروض، با دایرهٔ پیش مماس است و تمام این بیضی در داخل دایرهٔ C قرار دارد.
بنابراین، نقطهٔ مفروض مذکور، اوج قمر مصنوعی بر مدار است؛ و نقطهٔ مقابل، حضیض آن میباشد.
علل سقوط اقمار مصنوعی
معمولاً با سرعتهای کمتر از V۰، این مدارها «مدار ساقط» هستند. یعنی قمر مصنوعی معمولاً پس از چند بار گردش، مجدداً برروی سیاره S سقوط میکند.
[این مسأله، غالباً بهعلت وجود جوی بر روی سیارهٔ مفروض است، که هرگاه قمر مصنوعی در حرکت خود وارد جو سیاره شود، بهعلت مقاومت این جو، سرعت قمر مصنوعی میکاهد و بالاخره با کاهش متوالی این سرعت، قمر مصنوعی به علت جاذبهٔ سیاره به آن نزدیک میشود و در نتیجه سقوط میکند و یا در همان برخورد اول با جو، میسوزد.]
یک علت دیگر سقوط قمر مصنوعی این است که سیارهٔ مبداء، کرهٔ هندسی کامل نیست و با آن اختلاف دارد. زیرا محاسبات مدارهای اقمار مصنوعی، با این فرض که «سیارهٔ مبداء کروی است» صورت میگیرد؛ و اگر حاشیهٔ اطمینانی برای سرعت در نظر گرفته نشود، آخرالامر اختلالهائی که از اختلاف شکل سیارهٔ مبداء با «کرهٔ هندسی کامل» حاصل میشود، سرعت قمر را میکاهد.
مسلم است که اگر ارتفاع قمر مصنوعی بهقدر کافی زیاد باشد، یعنی قمر مصنوعی از سیارهٔ اصلی دور باشد، ممکن است برای سرعتهای کمتر از V۰ (ولی نزدیک بهآن) مدار بیضی قمر مصنوعی وارد جو سیارهٔ مبداء نشود. در این صورت فقط عامل دوم (یعنی اختلاف شکل کروی سیاره با کرهٔ هندسی) سرعت قمر را خواهد کاست. و این عامل، چندان مؤثر نیست و بنابراین، قمر مصنوعی، پیش از آن که ساقط شود، مدت مدیدی بهدور سیاره خواهد گشت.
این امر در اقمار مصنوعی امریکائی و شوروی رعایت شده است، و چنان که میدانیم، بسیاری از اقمار مصنوعی این دو کشور که به ماورای کرهٔ زمین پرتاب شدهاند مدتها بهدور زمین دوران کردهاند و یا میکنند.
مسیرهای «بالیستیک»
بههر اندازه که سرعت حرکت قمر مصنوعی در ارتفاع معین کمتر از V۰ باشد، بههمان میزان مدار قمر مصنوعی در نقطهٔ مقابل (یعنی نقطهٔ حضیض) به سیاره نزدیکتر میشود؛ بهقسمی که برای سرعتهای خیلی کم، مدار بیضی قمر مصنوعی، سطح سیاره را قطع میکند و چنین بهنظر میرسد که قمر مصنوعی از یک نقطهٔ سیاره پرتاب شده در نقطهٔ دیگری بهروی سیاره نشسته است. چنین مسیرهائی را مسیرهای بالیستیک مینامند.
بعدها توضیح خواهد شد که چگونه این مسیرهای بالیستیک برای تجربیات کپسولهای فضائی مورد استفادهٔ دانشمندان آمریکائی قرار گرفته است.
***
اگر فرض کنیم که سیارهٔ اصلی (سیارهٔ مبداء) دارای جوی است، میتوان حداقل سرعت حرکت قمر مصنوعی را در ارتفاع معینی بهدست آورد، بهقسمی که مسیر قمر (یعنی مدار آن) بهجو سیاره ورود نکند. در این صورت، مدارهای بیضی که در خارج این مدار واقعاند، مدارهای غیر ساقط میباشند (در اینجا از عامل اختلاف کرویت سیاره صرف نظر شده).
در شکل اول، کیفیت مدارهای بیضوی که در داخل مدار دایرهئی شکل قمر مصنوعی قرار دارند نشان داده شده است.
با سرعت V۰ در ارتفاع معین h، مدار دایره c میباشد.
سرعت V۱ حداقل سرعتی است که در ارتفاع h با آن سرعت قمر مصنوعی مدار بیضی شکل T۱ را میپیماید.
بیضی T۱ به جو سیاره ورود نمیکند و با آن مماس است.
مدارهای بیضی که بین T۱ و c واقعاند، مدارهای دوران میباشند (یعنی قمر مصنوعی برروی آنها به دور سیاره دوران میکند).
مدارهای بیضی که درون T۱ میباشند، مدارهای ساقط هستند (یعنی قمر مصنوعی بر روی این مدارها& معمولاً پس از چند گردش، بالمآل بر روی سیاره سقوط میکنند).
فرض کنیم که V۲ حداقل سرعتی است که مدار بیضی شکل قمر مصنوعی، در ارتفاع h با سطح سیاره مماس میشود؛ و این مدار بیضی شکل را T۲ مینامیم. مسیرهای بیضی که در اندرون بیضی T۲ واقعاند، به مسیرهای بالیستیک موسوماند.
***
توضیح – باید توجه شود که مثلاً در قسمت اخیر، مدار یا مسیر بالیستیک بهسطح سیاره برخورد میکند. بنابراین باید متوجه بود که وقتی گفته میشود مدار، نظیر سرعت V۰ در ارتفاع h، مراد ما پرتاب قمر مصنوعی در ارتفاع h باسرعت V۰ در امتداد عمود بر شعاع سیاره در همین نقطه میباشد. وگرنه، ارتفاع مسیر قمر یا مدار آن، ممکن است در نقطهٔ دیگری پس از حرکت کمتر از h یا بیشتر از آن شود (مگر در مسیر دایرهئی، که ارتفاع، همواره h میباشد).
خوانندگان، باتوجه به شکل یک، خود بهاین موضوع متوجه خواهند شد.
در این شکل، سطح خارجی سیاره و حد خارجی جو آن نشان داده شده است.
البته اگر سیارهئی دارای جوی نباشد، کلیهٔ بیضیهای مدار – بین بیضی T و دائرهٔ c – مدارهای دوران هستند. یعنی دیگر مدار ساقط وجود ندارد. مسیرهای قمر مصنوعی، یا مسیر بالستیک میباشند و یا مدارهای دوران.
[مجدداً یادآور میشویم که از عامل دوم سقوط مدارها – یعنی از اختلاف شکل سیاره با کرهٔ هندسی – چشمپوشی شده است.]
(بقیه دارد)